Historias del dekanato
El conocimiento no sirve de nada si no se comparte. En este espacio recopilamos aprendizajes, ideas y reflexiones sobre datos, tecnología, inteligencia artificial y negocio. Desde experiencias reales hasta estrategias aplicadas, queremos que este blog sea una fuente de inspiración y utilidad para quienes están construyendo el futuro con tecnología.
¿Qué son las alucinaciones en los modelos de lenguaje?9 junio 2025

En los últimos años, los modelos de lenguaje como GPT o Gemini han transformado radicalmente la forma en que interactuamos con la información. Sin embargo, pese a su capacidad para generar texto coherente y convincente, estos modelos no están exentos de errores. Uno de los más preocupantes es el fenómeno de las alucinaciones.
En este contexto, una alucinación es cuando el modelo genera una afirmación que parece plausible pero es falsa o no verificable. Es decir, el modelo "inventa información", aunque lo haga de forma gramaticalmente impecable.
El término proviene de la analogía con las alucinaciones humanas: percepciones sin estímulo externo. En los LLMs, ocurre algo similar: el modelo genera patrones sin anclarlos a hechos reales.
¿Por qué ocurre esto? Porque un modelo de lenguaje predice la siguiente palabra en una secuencia, maximizando la probabilidad condicional:
Este proceso no garantiza veracidad, solo coherencia estadística.
Las alucinaciones pueden clasificarse en intrínsecas (contradicen el input), extrínsecas (son incorrectas respecto al mundo) y contextuales (malinterpretan la conversación).
¿Cómo evitarlas? Algunas estrategias:
- RAG (Retrieval-Augmented Generation): el modelo consulta una base externa para responder con datos actualizados.
- Fine-tuning: afinar el modelo en dominios concretos reduce errores.
- Temperature baja: usar un valor bajo de reduce la creatividad pero también las invenciones.
Caso real: en 2023, el abogado neoyorquino Steven Schwartz usó ChatGPT para redactar un escrito legal. El modelo inventó seis casos judiciales. El juez lo descubrió y sancionó al abogado por fraude.
Conclusión: Las alucinaciones son una consecuencia directa del funcionamiento estadístico de los LLMs. Pueden mitigarse, pero no eliminarse por completo. Saber detectarlas es clave para un uso responsable de esta tecnología.
Cuatro paradojas que pueden engañarte con los datos14 mayo 2025

Los datos nos hablan, pero a veces, si no sabemos escucharlos con el rigor adecuado, nos pueden confundir. En el mundo del análisis cuantitativo y la toma de decisiones basadas en datos, hay paradojas que desafían la intuición y que, si no se entienden bien, pueden llevar a errores estratégicos graves. En este artículo exploramos cuatro de las más conocidas: Simpson, Berkson, la del Superviviente y Bonferroni.
Estas paradojas no son simples curiosidades estadísticas: son trampas reales en las que incluso los analistas más experimentados pueden caer. Entenderlas y saber detectarlas es una herramienta clave para cualquier empresa orientada a los datos. Al final, los datos no sólo hay que analizarlos, también hay que saber interpretarlos. Y para eso, la lógica no siempre basta: hace falta contexto, pensamiento crítico… y conocer estas paradojas.
Esta paradoja fue descrita por primera vez por Edward H. Simpson en 1951, aunque el fenómeno ya había sido observado anteriormente por Pearson y Yule a principios del siglo XX. Se da cuando una tendencia aparente en varios grupos de datos desaparece o incluso se invierte al agregarlos.
El caso más famoso ocurrió en 1973 con las admisiones de posgrado en la Universidad de Berkeley. Las estadísticas globales parecían mostrar que se discriminaba a las mujeres. Pero al analizar los datos por departamento, se descubrió que en la mayoría de ellos las mujeres eran admitidas en mayor proporción. El sesgo se debía a que las mujeres solicitaban más en departamentos altamente competitivos, mientras que los hombres lo hacían en los más accesibles.
Otro ejemplo clásico es en sanidad: un tratamiento puede parecer más efectivo en hombres y en mujeres por separado, pero menos efectivo en el total si las proporciones de cada grupo están desequilibradas.
¿Qué aprendemos? Nunca analices una media global sin estudiar los subgrupos. La segmentación es clave. En dashboards y modelos, verifica si los patrones globales se replican en los segmentos.
Esta paradoja fue formulada por el estadístico Joseph Berkson en 1946 mientras trabajaba en el Hospital Mayo Clinic. Observó que cuando se analizaban solo pacientes hospitalizados, aparecían relaciones negativas entre enfermedades que no existían en la población general.
Imagina que estás estudiando la relación entre el tabaquismo y la obesidad, pero solo entre pacientes ingresados. Puede parecer que hay una correlación negativa (los obesos fuman menos), pero es una ilusión: ambos factores aumentan el riesgo de ingreso, y la observación está sesgada por el hecho de que solo miramos a los hospitalizados.
Otro ejemplo actual: al analizar usuarios activos de una app, puedes pensar que los que más pagan son los que menos la usan, porque sólo ves a los que siguen activos. Pero estás dejando fuera a los que pagaron y se fueron.
¿Qué aprendemos? Cuidado con las correlaciones artificiales cuando estás trabajando con datos filtrados. El sesgo de selección puede estar escondido en muchas bases de datos reales.
Esta paradoja es tan poderosa como sutil. Fue formalmente enunciada en la Segunda Guerra Mundial, gracias al análisis de Abraham Wald, un matemático húngaro que trabajaba en problemas estadísticos militares en EE.UU.
Cuando los aviones regresaban con impactos de bala, el Ejército pensó que debía reforzar esas zonas. Wald, sin embargo, señaló que esos eran los aviones que habían sobrevivido. Las zonas sin impactos visibles eran probablemente aquellas que, si eran alcanzadas, causaban la destrucción del avión. Por tanto, esas debían reforzarse.
Esta idea se ha aplicado en finanzas (analizar solo empresas que han sobrevivido a varias crisis), educación (evaluar programas solo con estudiantes que se gradúan) y negocios (analizar solo clientes actuales). En todos los casos, se ignora lo que no está en la muestra, y eso puede distorsionar por completo la conclusión.
¿Qué aprendemos? No todo lo que importa está en los datos visibles. Los ausentes —los que no llegaron, no sobrevivieron o abandonaron— también cuentan.
Carlo Emilio Bonferroni fue un matemático italiano que en 1935 propuso una forma de ajustar la significación estadística cuando se realizan múltiples comparaciones. Su fórmula protege contra los falsos positivos que aparecen cuando se hacen muchos tests estadísticos simultáneos.
Por ejemplo, si haces 100 tests con un nivel de significación de , esperarías encontrar 5 resultados "significativos" sólo por azar. La corrección de Bonferroni propone ajustar el umbral dividiendo por el número de comparaciones:
Así, si y , solo consideras significativos los resultados con .
Esto es vital en ciencia, pero también en marketing, analítica web, A/B testing y dashboards interactivos donde se prueban decenas de hipótesis a la vez. Si no corriges, es probable que tomes decisiones basadas en resultados que son puro azar.
¿Qué aprendemos? En contextos de exploración intensiva de datos, es crucial ajustar tu criterio de significación. Si no, acabarás creyendo cosas que no son.
LLMs multimodales: hacia una inteligencia general integradora21 abril 2025
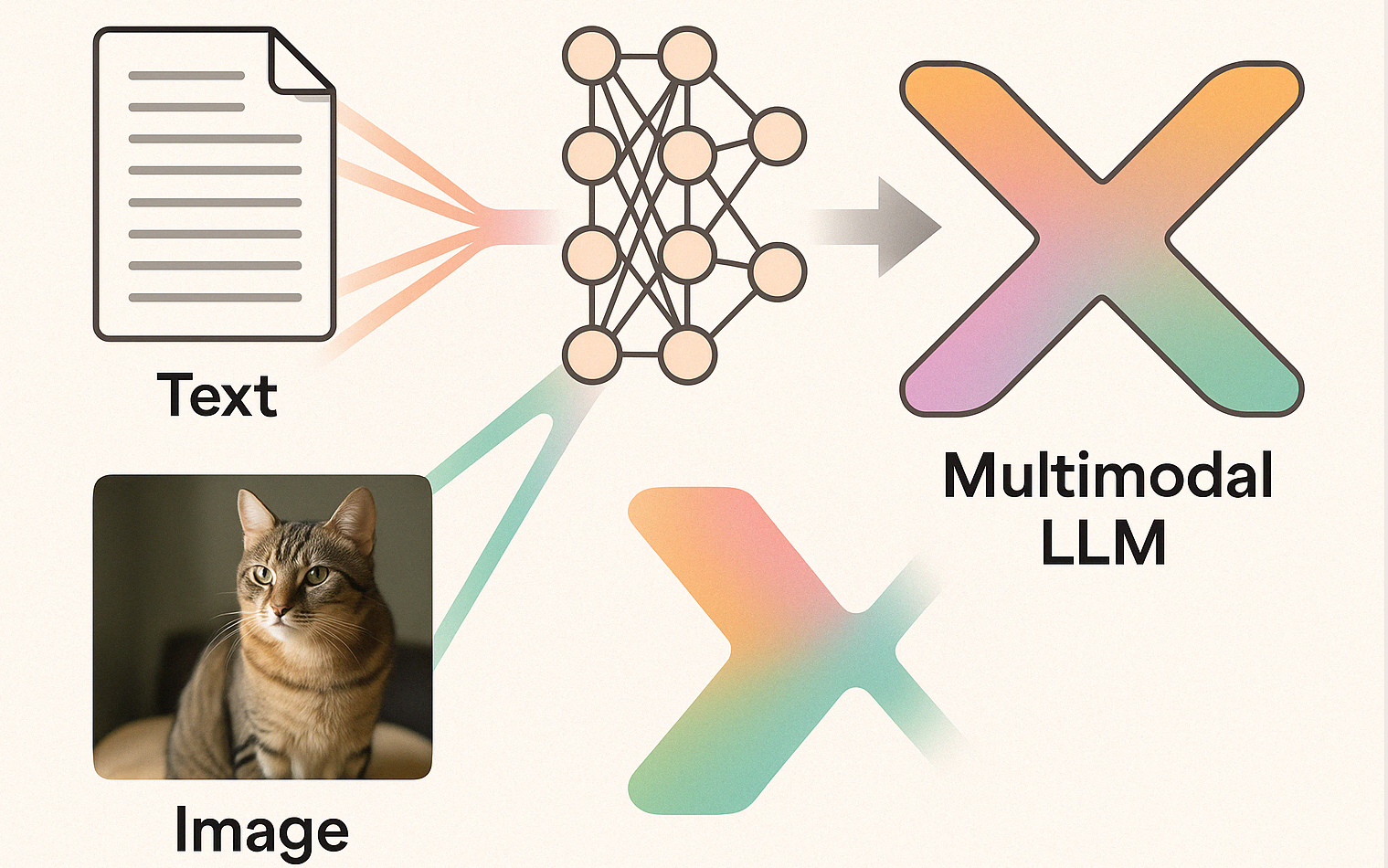
Este documento tiene como objetivo proporcionar un estudio técnico y riguroso sobre los modelos de lenguaje multimodales (Multimodal Large Language Models, MLLMs), una de las líneas de desarrollo más activas y prometedoras en inteligencia artificial en 2025. A diferencia de los modelos unimodales, los MLLMs tienen la capacidad de recibir, integrar y razonar sobre múltiples tipos de datos —texto, imágenes, audio, vídeo, representaciones espaciales o acciones motoras— utilizando una arquitectura unificada. Esta capacidad de operar sobre distintas fuentes de información y de extraer representaciones semánticas conjuntas es una de las claves hacia la construcción de sistemas verdaderamente generalistas o incluso proto-AGI (Artificial General Intelligence).
A lo largo de este artículo desgranaremos la estructura matemática, arquitectónica y computacional que subyace a estos modelos. Empezaremos por el problema de la alineación de espacios latentes entre modalidades, avanzaremos por las técnicas de entrenamiento generativo y discriminativo, exploraremos la geometría del embedding multimodal y discutiremos las métricas formales para cuantificar la capacidad representacional multimodal. Finalizaremos con una discusión de los retos técnicos y filosóficos, y sus implicaciones para el diseño de arquitecturas futuras.
Desde el punto de vista estadístico, cada modalidad puede considerarse una variable aleatoria definida sobre un espacio de probabilidad distinto. Denotemos por una variable que representa imágenes (por ejemplo, en ), y por una variable textual (por ejemplo, una secuencia de tokens en un espacio discreto ).
La multimodalidad implica que existe una dependencia estadística entre estas variables, es decir, su distribución conjunta no se factoriza. El objetivo de los modelos multimodales es precisamente aprender esa estructura conjunta, bien modelando explícitamente (modelo generativo), bien aprendiendo una función que capture su dependencia funcional (modelo discriminativo), o bien ambos simultáneamente.
Desde una perspectiva geométrica, cada modalidad define un manifold de alta dimensión con propiedades topológicas y métricas distintas. La tarea del encoder multimodal es encontrar una inmersión diferenciable tal que las representaciones correspondientes a datos semánticamente similares queden próximas en . Esta es la base de los llamados "espacios latentes compartidos".
Los encoders multimodales más utilizados (ViT, CLIP, ResNet, Swin Transformers para imagen; Transformers para texto) se entrenan de forma conjunta para alinear las representaciones mediante pérdidas contrastivas. La función de pérdida más común es InfoNCE, que busca maximizar la similitud entre pares positivos y minimizarla para negativos.
Dado un batch de pares , la formulación es:
Aquí, suele ser la similitud coseno. El parámetro es una temperatura que controla la dispersión. Esta pérdida se puede derivar como una cota inferior de la información mutua entre variables latentes, tal como se muestra en [5].
Un aspecto crítico es que estas pérdidas inducen una métrica en que no necesariamente conserva la semántica local en cada modalidad. Esto ha llevado al desarrollo de técnicas como Modality Alignment Regularization o Geometry-Preserving Embeddings.
Los MLLMs más avanzados como GPT-4V o Gemini adoptan arquitecturas autoregresivas que modelan explícitamente la probabilidad condicional , donde puede ser una imagen, vídeo o secuencia de instrucciones, y una secuencia textual.
Esto se implementa concatenando los embeddings de entrada de distintas modalidades en una única secuencia de tokens procesada por un Transformer. El modelo entonces maximiza:
Este paradigma permite realizar tareas como captioning, VQA (Visual Question Answering), razonamiento visual-matemático, seguimiento de instrucciones con contexto visual, y más.
Si concebimos como una variedad diferencial con una métrica Riemanniana inducida por los gradientes del modelo, podemos analizar la curvatura local, las trayectorias de interpolación y la capacidad del modelo para representar trayectorias semánticas continuas.
Por ejemplo, dados dos puntos y , se puede definir una curva geodésica tal que y , y su longitud está dada por:
donde es la métrica inducida por el Jacobiano de o . Esta formulación permite estudiar propiedades como la isometría local entre modalidades, crucial para tareas de interpolación semántica.
Para cuantificar la capacidad de un modelo multimodal se han propuesto métricas basadas en teoría de la información, como la información mutua empírica, la entropía cruzada multimodal o la divergencia de Jensen-Shannon entre distribuciones condicionadas. También se utilizan métricas geométricas como el radio de curvatura local promedio, la entropía de la distribución de embeddings y la densidad modal en espacios latentes.
Uno de los desarrollos más prometedores en el campo de los modelos multimodales es su integración dentro de agentes cognitivos artificiales. Un agente multimodal no solo interpreta entradas diversas, sino que las utiliza en tiempo real para tomar decisiones, planificar, interactuar con herramientas y mantener una representación interna coherente de su entorno. Para ello, el modelo debe incorporar mecanismos de memoria de corto y largo plazo.
Desde el punto de vista formal, podemos modelar un agente como una función de política , donde es el historial multimodal hasta el tiempo y es el conjunto de acciones posibles. A diferencia de los modelos tradicionales de NLP, que operan sobre entradas acotadas, aquí crece dinámicamente.
Esto requiere estructuras especializadas como:
- Memorias vectoriales persistentes: embeddings almacenados con mecanismos de atención diferenciable (como en MemNet, RETRO, o KNN-Mem).
- Contextos jerárquicos temporales: Transformers de memoria jerárquica (HTM) que condensan múltiples niveles de representación (token, segmento, sesión).
- Planificadores neuro-simbólicos: arquitecturas que combinan modelos generativos con motores de lógica simbólica para razonamiento sobre estados y metas.
El reto consiste en definir mecanismos de actualización de memoria que preserven coherencia semántica y eficiencia computacional. Formalmente, se modela como un proceso de proyección adaptativa:
El verdadero potencial de los MLLMs se revela cuando no solo reciben información pasiva, sino que interactúan activamente con su entorno. Esto requiere un mecanismo de grounding semántico: la capacidad del modelo para vincular conceptos internos con referencias observables en el mundo físico.
Desde la filosofía del lenguaje hasta la semántica computacional, el grounding ha sido uno de los temas más debatidos. En modelos multimodales, se plantea como el problema de mapear tokens abstractos a entidades observables con las que el modelo puede interactuar. Este mapeo es dinámico, contextual y dependiente de la memoria del agente.
Formalmente, se puede definir como una función de atención semántica sobre el estado del mundo :
donde es el embedding del concepto y la representación del objeto en el contexto actual.
A diferencia del aprendizaje en batch típico de los LLMs, los agentes multimodales operan en entornos no estacionarios. Esto requiere mecanismos de aprendizaje en línea, donde los pesos del modelo o sus componentes de memoria se actualizan continuamente a medida que el agente observa nuevas entradas. Algunos enfoques actuales incluyen:
- Meta-learning en línea: utilizar modelos de segundo orden para ajustar los pesos rápidamente con pocos ejemplos (p. ej., MAML, Reptile).
- Sinapsis dinámicas: mecanismos inspirados en neurociencia que modulan la plasticidad local de las conexiones neuronales en función del contexto.
- Aprendizaje bayesiano secuencial: modelos de inferencia variacional que actualizan distribuciones sobre parámetros en tiempo real.
El principal desafío es evitar el catastrophic forgetting, fenómeno donde el modelo olvida tareas previas al adaptarse a nuevas. Esto ha motivado el desarrollo de métodos de consolidación de memoria como EWC (Elastic Weight Consolidation) o replay generativo multimodal.
La integración de múltiples canales sensoriales, memoria episódica, aprendizaje continuo y grounding semántico en un solo sistema ha sido durante décadas uno de los objetivos principales de la inteligencia artificial general. Desde la perspectiva de Marr, los MLLMs permiten una implementación funcional de los niveles computacional, algorítmico y físico de la cognición artificial.
Sin embargo, la pregunta sigue abierta: ¿basta con escalar estos sistemas para alcanzar una forma de inteligencia general, o es necesario un cambio cualitativo en su arquitectura? Las limitaciones actuales en razonamiento causal, autonomía, modelado explícito de creencias y comprensión contrafactual sugieren que la multimodalidad es una condición necesaria pero no suficiente.
La verdadera AGI, en este marco, requeriría modelos que no solo representen correlaciones entre inputs, sino que construyan modelos internos del mundo, formulen hipótesis, simulen futuros alternativos y tomen decisiones de forma autónoma y explicable. Los MLLMs actuales constituyen un paso clave en esa dirección, pero su evolución futura probablemente integrará elementos simbólicos, neurobiológicos y metacognitivos.
[1] CLIP: Radford et al., 2021
[2] Flamingo: DeepMind, 2022
[3] Gemini: DeepMind, 2024
[4] Claude 3: Anthropic, 2024
[5] Representation Learning with Contrastive Predictive Coding (Oord et al., 2018)
[6] Attention Is All You Need (Vaswani et al., 2017)
[7] Meta-Learning with Differentiable Convex Optimization (Finn et al., 2017)
Modelos de difusión para generación de imágenes: una visión técnica3 abril 2025

En los últimos años, los modelos de difusión se han consolidado como la arquitectura dominante en la generación de imágenes de alta fidelidad. Herramientas como DALL·E 3, Stable Diffusion o Imagen (de Google) han demostrado gran capacidad para transformar texto en imágenes. Como físico y data scientist, encuentro especialmente interesante que este paradigma se base en conceptos que recuerdan a la física estadística: evolución estocástica, procesos reversibles y manipulación controlada del ruido gaussiano. Este artículo tiene como objetivo desentrañar el funcionamiento interno de los modelos de difusión desde una perspectiva técnica, conectando ideas del aprendizaje profundo con fundamentos matemáticos y físicos.
La idea detrás de los modelos de difusión puede parecer contraintuitiva al principio: en lugar de aprender directamente a generar una imagen desde cero, el modelo aprende a revertir un proceso que añade ruido progresivamente a una imagen real, hasta convertirla en puro ruido gaussiano. Este proceso de degradación se llama forward diffusion, y se modela como una cadena de Markov:
donde es la imagen original (una muestra del dataset), es la cantidad de ruido añadido en el paso t, normalmente con valores crecientes en el tiempo y es la imagen degradada tras t pasos. La distribución marginal, es decir, el estado de la imagen tras t pasos partiendo de la original, se puede calcular de forma cerrada:
donde . Este proceso es conceptualmente similar a un sistema físico en contacto con un baño térmico: con cada paso, se incrementa su entropía hasta alcanzar un estado de máximo desorden (ruido blanco).
La clave de estos modelos es que aprenden una aproximación del proceso inverso:
donde \theta representa los parámetros de una red neuronal entrenada para predecir cómo pasar de una imagen ruidosa a una versión ligeramente menos ruidosa . Esta red normalmente es una U-Net con atención, que capta tanto patrones locales como relaciones globales. En lugar de predecir directamente , muchos modelos (como los descritos en Ho et al., 2020 ) prefieren predecir el ruido añadido en cada paso. Esto simplifica el entrenamiento y mejora la estabilidad:
donde es ruido gaussiano. Este proceso inverso puede verse como una especie de dinámica de Langevin inversa, donde el modelo aprende a navegar desde un estado de máxima entropía hacia un estado ordenado, en una trayectoria guiada por el aprendizaje estadístico.
Para generar imágenes desde texto, como hace DALL·E 3, el proceso de difusión se condiciona a una descripción textual . Esta se representa como un embedding semántico extraído por un modelo de lenguaje (generalmente un Transformer), y se introduce en la red de difusión para guiar la reconstrucción. Formalmente, el modelo ahora aprende:
Este conditioning se puede introducir mediante concatenación del embedding textual a los mapas de características, cross-attention en múltiples capas de la U-Net o FiLM layers o conditioning tokens. Lo importante es que el modelo aprende a deshacer el ruido no solo de forma coherente visualmente, sino también coherente semánticamente con el texto proporcionado. Este diseño es la base de los modelos como DALL·E 2 y 3 [2] y la serie de modelos Imagen de Google [3].
donde es ruido gaussiano. Este proceso inverso puede verse como una especie de dinámica de Langevin inversa, donde el modelo aprende a navegar desde un estado de máxima entropía hacia un estado ordenado, en una trayectoria guiada por el aprendizaje estadístico.
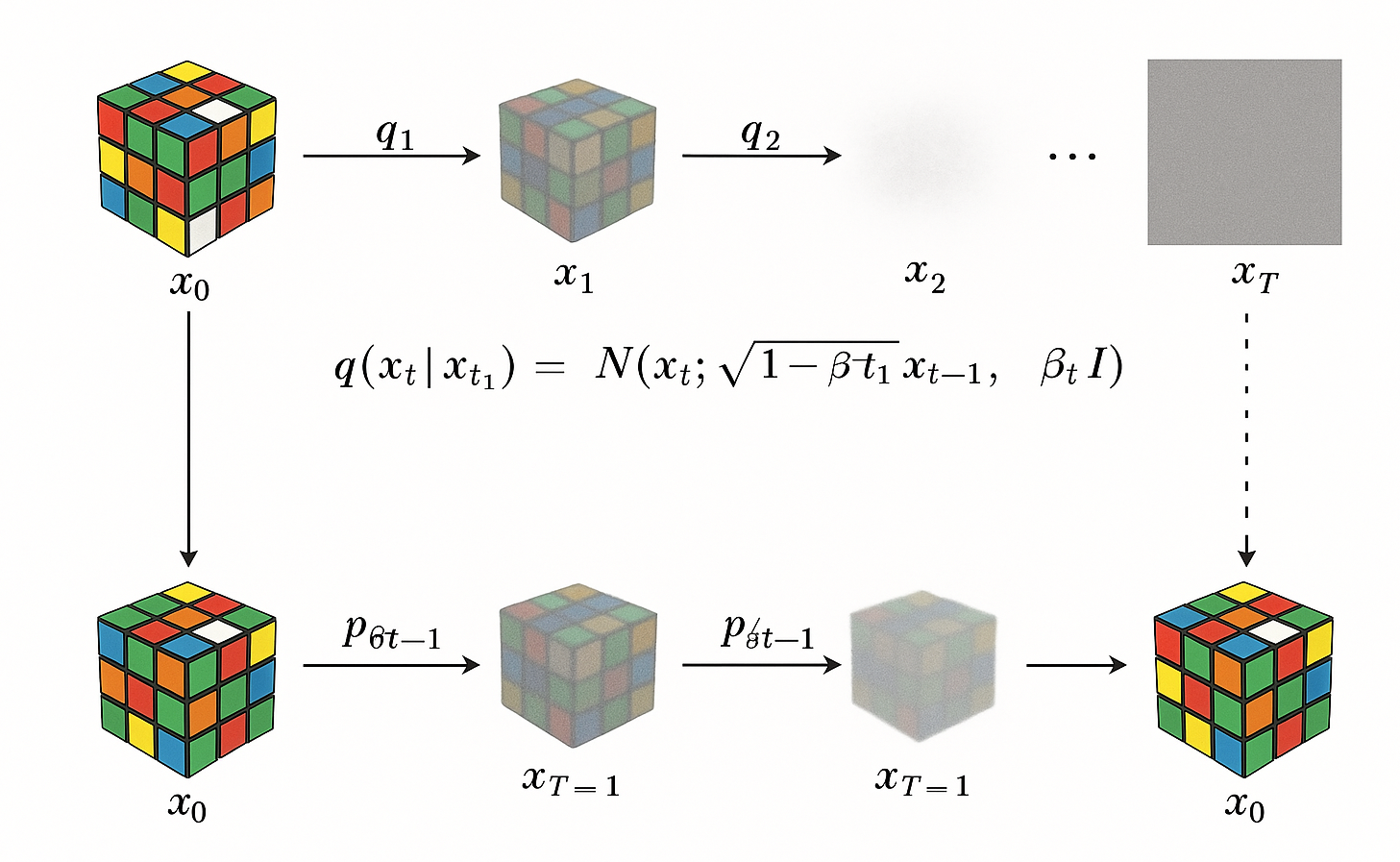
Uno de los desafíos prácticos de estos modelos es que el sampling requiere recorrer la cadena de Markov inversa paso a paso - originalmente con hasta 1000 pasos. Esto es lento y computacionalmente costoso, aunque se han propuesto múltiples mejoras:
- DDIM [4]: permite sampling determinista y acelerado
- PLMS / DPM-Solver [5]: reduce pasos sin sacrificar calidad
- Latent Diffusion Models (LDM) [6]: realizan la difusión en un espacio latente comprimido aprendido por un autoencoder, lo que reduce enormemente el coste computacional.
Este último enfoque es el que utiliza Stable Diffusion, haciendo viable la generación de imágenes en GPU de consumo.
Una de las razones por las que los modelos de difusión me resultan especialmente elegantes es por su profunda resonancia con ideas de la física estadística. Al margen de su efectividad empírica, estos modelos se alinean de forma sorprendente con procesos físicos conocidos, desde la evolución de sistemas fuera del equilibrio hasta la integración de trayectorias estocásticas guiadas por un potencial.
El forward process como difusión térmica
El proceso directo (forward diffusion) puede interpretarse como una difusión térmica gaussiana, análoga al comportamiento de un sistema físico sometido a ruido térmico creciente.
Recordemos que en el forward process:
Este tipo de dinámica es equivalente a una ecuación de Langevin discreta donde se introduce ruido a cada paso, lo cual es físicamente equivalente a modelar una partícula en un medio con temperatura creciente. La imagen original representa un estado ordenado de baja entropía, y el proceso de difusión lo lleva a un estado máximo de entropía (ruido blanco), es decir, una térmica asintótica.
El proceso inverso como dinámica de Langevin reversa
Aquí entra en juego lo realmente interesante: ¿cómo se puede invertir ese proceso de entropía creciente? En el trabajo de Song [7], el proceso inverso se modela como una ecuación diferencial estocástica (SDE):
donde es el drift (típicamente cero en el caso de ruido isotrópico), escala el ruido y es un proceso de Wiener (movimiento browniano).
Aquí es donde entra la red neuronal: el modelo no aprende directamente , sino que aprende a estimar ese score function, que actúa como un campo de fuerzas que guía la partícula (o imagen) de vuelta al orden.
Este procedimiento recuerda a técnicas de simulación estocástica inversa en física computacional, donde se intenta reconstruir trayectorias plausibles a partir de estados observados, en ausencia de ecuaciones exactas.
Ecuaciones de Fokker–Planck y evolución de distribuciones
La evolución de la densidad de probabilidad de las imágenes durante la difusión puede describirse mediante la ecuación de Fokker–Planck, que formaliza cómo cambia en el tiempo bajo un SDE:
El proceso inverso, por tanto, consiste en deshacer esta evolución de la densidad, lo cual es en general intratable de forma analítica, pero si se puede estimar el score , se puede construir una SDE inversa que efectivamente lo revierta. Ésta es la base de los Score-Based Generative Models, que reinterpretan los modelos de difusión como integración de una trayectoria estocástica condicionada al score aprendido.
Potencial de energía y generación dirigida
Desde una visión más general, el modelo aprende un paisaje de energía en el espacio de imágenes, definido por la densidad , y genera muestras siguiendo una dinámica que minimiza esa energía. La relación entre la densidad y la energía se da por:
Por tanto, el score function representa una fuerza que empuja las muestras hacia regiones de baja energía (alta probabilidad). Esta idea tiene una resonancia directa con sistemas físicos que evolucionan hacia estados de mínima energía libre.
[1] - Denoising Diffusion Probabilistic Models (Ho et al., 2020)
[2] - Hierarchical Text-Conditional Image Generation with CLIP Latents (DALL·E 2) (Ramesh, A. et al., 2022)
[3] - Imagen: Text-to-Image Diffusion Models (Saharia, C. et al. , 2022)
[4] - High-Resolution Image Synthesis with Latent Diffusion Models (Rombach, R. et al., 2022)
[5] - Score-Based Generative Modeling through Stochastic Differential Equations (Song, Y. et al., 2021)
[6] - Denoising Diffusion Implicit Models (Song, Y., & Ermon, S., 2020)
[7] - DPM-Solver: A Fast ODE Solver for Diffusion Probabilistic Models (Lu, C. et al., 2022)
De máquinas tontas a inteligencia conversacional: la revolución de los LLMs20 febrero 2025

Si hace unos años alguien me hubiera dicho que podría tener conversaciones fluidas con una inteligencia artificial, le habría respondido que no vivimos en "Matrix". Porque hasta hace poco, las "IAs" con las que interactuábamos no eran más que sistemas con reglas rígidas y respuestas predefinidas, nada sofisticado ni parecido al "Arquitecto", volviendo a la referencia de Matrix. Los chatbots no entendían lo que decíamos, simplemente buscaban patrones en las frases y respondían con un guion programado, y los traductores automáticos funcionaban más por reglas gramaticales y diccionarios que por verdadera comprensión del lenguaje. Entonces, llegaron los LLMs (Large Language Models) y lo cambiaron todo.
Un Large Language Model es un tipo de inteligencia artificial entrenado con redes neuronales profundas para procesar y generar texto de manera coherente y contextual. Antes, los sistemas de IA dependían de programación explícita: si querías que un asistente virtual respondiera preguntas sobre el clima, tenías que escribir reglas como: Si el usuario pregunta “¿Va a llover mañana?”, busca la información en la base de datos del tiempo y devuelve la respuesta. Si la pregunta era ligeramente diferente (”¿Qué tiempo hará mañana?”), la IA podía fallar porque no reconocía la estructura exacta. Los LLMs, en cambio, no funcionan con reglas predefinidas, sino que aprenden patrones directamente del lenguaje humano. Son modelos entrenados con miles de millones de palabras para predecir cuál es la siguiente palabra más probable en una frase. Este enfoque les permite adaptarse a múltiples tareas sin necesidad de ser programados específicamente para cada una, lo que nos lleva a la siguiente pregunta: ¿Cómo se entrenan esos modelos?
El entrenamiento de un Large Language Model ocurre en dos fases principales: el pre-entrenamiento y el fine-tuning. En la primera fase, el modelo se expone a enormes cantidades de texto (libros, artículos, conversaciones en internet, documentación técnica, entre otros) y aprende a identificar patrones lingüísticos sin una comprensión real del significado. Para lograrlo, utiliza una arquitectura llamada Transformers, que permite analizar relaciones entre palabras a larga distancia dentro de una oración y procesar enormes volúmenes de datos en paralelo [1]. Básicamente, el modelo aprende a predecir cuál es la siguiente palabra más probable en una secuencia, ajustando sus pesos neuronales a medida que mejora en esta tarea. Este proceso requiere una capacidad computacional gigantesca, con clusters de GPUs y TPUs funcionando durante semanas o meses para afinar los billones de parámetros que conforman el modelo.
Después del pre-entrenamiento, el modelo pasa por una fase de ajuste llamada fine-tuning, donde se optimiza para tareas específicas y se corrige su comportamiento. En este punto, los investigadores aplican técnicas como el aprendizaje por refuerzo con retroalimentación humana (RLHF), donde expertos evalúan las respuestas del modelo y lo guían para ser más preciso, útil y seguro. Esta fase es clave para reducir sesgos, evitar respuestas dañinas y mejorar la alineación del modelo con el tipo de información que se espera de él.
Es aquí donde un LLM deja de ser un simple generador de texto y se convierte en una herramienta sofisticada capaz de asistir en tareas complejas como redacción técnica, generación de código, razonamiento lógico o incluso asesoramiento en distintos campos.
Hoy, los LLMs no solo han superado las limitaciones de los antiguos chatbots y sistemas de reglas fijas, sino que han redefinido la forma en que interactuamos con la tecnología. Ya no se trata de simples asistentes que siguen instrucciones básicas, sino de modelos capaces de generar ideas, estructurar conocimiento y, en muchos casos, sorprendernos con su aparente comprensión del mundo. No estamos en Matrix, pero hemos dado un salto cualitativo en nuestra relación con la inteligencia artificial, acercándonos a un futuro donde la comunicación con las máquinas es más fluida, natural y poderosa que nunca. La pregunta ya no es si los LLMs cambiarán la forma en que trabajamos, sino cómo aprovecharemos esta nueva era de la IA para potenciar nuestra creatividad, eficiencia y capacidad de innovación.
